Ola Widlund: MHD

January 14, 2005: This page is under construction...
More information on this topic is available in the references below.
You are also welcome to contact me by e-mail.

/Ola

Modeling of MHD turbulence

MHD turbulence

Fluid flow turbulence subjected to a magnetic field will experience magnetic dissipation, or Joule dissipation. While ordinary viscous dissipation acts primarily on the smallest eddies, magnetic dissipation selectively affects turbulent structures depending on their geometrical shape. Isotropic turbulent structures are effectively dissipated, while cigar-shaped structures aligned with the magnetic field lines are only weakly affected. The observed behavior is therefor that turbulence is dissipated in a magnetic field, but also that the turbulent field at the same time becomes more and more two-dimensional, with eddies elongated in the direction of the magnetic field. As these anisotropic eddies are more resistant, the dissipation rate tends to diminish with time.

Theoretical arguments can be used to show that the Joule dissipation, , of turbulent kinetic energy , K, scales as

(1)

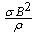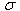where sigma*B^2/rho is the inverse of a magnetic timescale, while L_par and L_norm are characteristic turbulent length scales in the directions parallel and normal, respectively, to the magnetic field (B is the magnetic flux density, sigma is the fluid electric conductivity and rho the fluid density). The dependence on the ratio of length scales clearly demonstrates that the geometrical shape or structure of the turbulent eddies has a decisive role to play in MHD turbulence. The problem is that this kind of structure information is absent from all conventional turbulence models, be it eddy-viscosity closures like the k-epsilon model, or full Reynolds-stress models.

Modeling approach

The idea behind the MHD turbulence models discussed here is to introduce a minimum of the structure information necessary to describe MHD turbulence. We do this by defining a new transported turbulence variable called 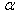alpha , such that the Joule dissipation of turbulent kinetic energy can be expressed exactly as

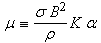(2)

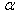A comparison with (1) suggests that alpha scaling in length scales , so that alpha can be interpreted as a dimensionality or structure anisotropy variable.

In the case of homogeneous turbulence, 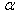alpha can be given an exact definition for which an exact transport equation can be derived from the Navier-Stokes equations. All source and sink terms in this equation are rather complicated and must be modeled. There are however plenty of well-proven tools from conventional turbulence theory that can be used to study the properties of these terms. We can for example use linear theory and rapid distortion theory to study the effect of a magnetic field on 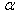alpha , and we can use direct numerical simulations (DNS) or large eddy-simulations (LES) to understand nonlinear effects.

The simplest model of this kind is the K-epsilon-alpha model, which is based on the standard K-epsilon model, extended with an equation for 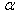and the necessary magnetic sink terms in the K epsilon equations. The three transport equations are

		(3)
		(4)
		(5)

As for the standard K-epsilon model, the turbulence production is given by

, with

(6)

and the turbulent viscosity is calculated as

(7)

The Joule dissipation term in the K equation is given by (2) and requires no modeling. The corresponding Joule destruction term in the epsilon equation is modeled as

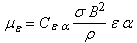(8)

where 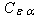C_epsalpha is a new model constant. This is simply a rescaling of (2), in the same logic as both the production and viscous terms in (4) are rescaled versions of the corresponding terms in the K equation (3).

Apart from the conventional transport terms, the proposed alpha equation contains a magnetic destruction term mu_alpha and a "return-to-isotropy" term pi_alpha representing nonlinear inertial effects. The exact alpha equation contains also terms depending on mean shear and strain, but they have been dropped from the model equation (5). The most obvious argument for this is that conventional models neglect the effects of structural effects altogether.

The magnetic destruction term mu_alpha is modeled with a piece-wise polynomial function fitted to exact results from linear theory (assuming a strong magnetic field and negligible nonlinear effects) :

(9)

The model term pi_alpha is based on recent results from direct numerical simulations, and takes the form

(10

with

	,	(11)
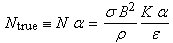	,	(12)

and model constants C_alpha2 and C_N .

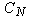The conventional part of the model uses the "standard" values for all constants:

(13)

The new model constants relevant to magnetic effects take the values

(14)

Performance of the model

There is almost no experimental data available to support a rigorous experimental validation of this kind of turbulence model. This is of course due to the extreme difficulties involved in measuring turbulent statistics, or even global mean flow properties, in a liquid metal. One of the few experiments done on decay of homogeneous turbulence in a magnetic field is that of Alemany et al. in 1979. There is a much larger volume of experimental data on MHD channel flows, with measurements of mean flow profiles and wall friction coefficients. Unfortunately the properties of MHD channel flows are determined largely by the boundary layers, and they are therefor not a very sensitive test for a turbulence model. The most challenging tests for this type of model is instead against various theoretical predictions of the properties of homogeneous turbulence subjected to a magnetic field.

If the magnetic field is strong enough, we can neglect inertial nonlinear effects. Under certain conditions the resulting linearized Navier-Stokes and Maxwell equations can be solved. Moffatt cold thus show that the kinetic energy of homogeneous turbulence decaying in a magnetic field should decay as ....

...To be continued (16/01/2005)...

Modeling of MHD turbulence

MHD turbulence

Modeling approach

Performance of the model

Other models of the same type

Further reading