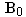.
Ohm's law then gives the electrical current asAssuming we want to simulate MHD flows with an existing general flow solver (e.g. Fluent, CFX or Star-CD), we need to add a minimum of electromagnetic equations. If the externally applied magnetic field is alternating (AC), one would probably choose to implement the induction equation for the three components of the induced magnetic field. If the magnetic field is static (DC), however, we can get away with solving only for scalar electrostatic potential. In the following I will limit myself to the DC case.
In steel casting, the fluid
flow
can be considered to
be incompressible
and Newtonian. The so-called magnetic Reynolds number is
usually well below unity, so that the distortion of the magnetic field
caused by the fluid flow remains small compared with the applied
external field, .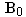
Ohm's law then gives the electrical current as
| |
 ,
|
(1) |
where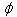
is the
electric
potential, 
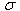is
the electrical conductivity and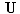 
is
the velocity. We can assume
that electrical charge is conserved, so
that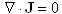 
.
Together with (1) this gives a Poisson equation for
the electric potential,
| |
 . |
(2) |
Once the electric potential is known, the electric current is given by (1) and the Lorentz force acting on the fluid can be computed as
| |
 . |
(3) |
In most general flow solvers the Poisson-type equation (2) for electric potential can be implemented as a generic transport equation, with transient and convection terms switched off.
In a staggered grid
arrangement a correct, current-conserving discretisation of the
equation would usually
follow naturally, with the electric potential given in the scalar
nodes, while potential gradient and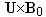 
-terms
are computed on the
vector nodes on control-volume faces.
An accurate discretisation is
less obvious in a co-located variable
arrangement. To avoid large errors, the 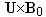-term
should be calculated
with interpolated velocities on the control-volume faces.
Cell-centre values of both current and Lorentz force are then computed
as averages of the facial values.
The discretisation in a co-located control-volume arrangement is
discussed
at length in the technical report cited below.